描述

一条单向的铁路线上,依次有编号为 1, 2, ..., n 的 n 个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。

(注意:起始站和终点站自然也算作事先已知需要停靠的站点)

例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。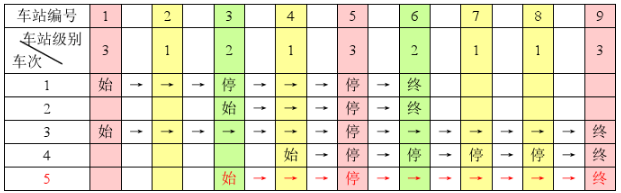

现有 m 趟车次的运行情况(全部满足要求),试推算这 n 个火车站至少分为几个不同的级别。

格式

输入格式

第一行包含 2 个正整数 n, m,用一个空格隔开。

第 i + 1 行(1 ≤ i ≤ m)中,首先是一个正整数 s i (2 ≤ s i ≤ n),表示第 i 趟车次有 s i 个停靠站;接下来有 s i 个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

输出只有一行,包含一个正整数,即 n 个火车站最少划分的级别数。

样例1

样例输入1

9 24 1 3 5 63 3 5 6

样例输出1

2

样例2

样例输入2

9 34 1 3 5 63 3 5 63 1 5 9

样例输出2

3

限制

每个测试点1s。

提示

对于 20%的数据,1 ≤ n, m ≤ 10;

对于 50%的数据,1 ≤ n, m ≤ 100;

对于 100%的数据,1 ≤ n, m ≤ 1000

来源

NOIP 2013 普及组

易知从起点到终点停靠的车站比未停靠的车站级别高

由大小关系想到拓补排序

然后标记一下次数取最大值就可以了

#include
    
     #include
     
      const int len=5000;int mm[1010];int qu[len];int tar[1010];int in[1010];int map[1010][1010];int main(){	int n,m;	scanf("%d %d",&n,&m);	for(int i=1;i<=m;i++)			{		int k;scanf("%d",&k);		for(int j=1;j<=k;j++)	scanf("%d",&mm[j]),tar[mm[j]]=i;		for(int j=mm[1];j<=mm[k];j++)			if(tar[j]!=i)		for(int t=1;t<=k;t++)		if(!map[j][mm[t]])	map[j][mm[t]]=1,in[mm[t]]++;	}	memset(tar,0,sizeof(tar));	int head=1,tail=2;	for(int i=1;i<=n;i++)	if(!in[i])	qu[tail++]=i,tar[i]++;	while(head<=tail)	{		int rr=qu[head++];if(head==len)	head=1;		for(int i=1;i<=n;i++)			if(map[rr][i])				if(!--in[i])					{					qu[tail++]=i;if(tail==len)	tail=1;	tar[i]=tar[rr]+1;				}	}	int max=0;	for(int i=1;i<=n;i++)	max=max>tar[i]?max:tar[i];	printf("%d\n",max);	return 0;}